

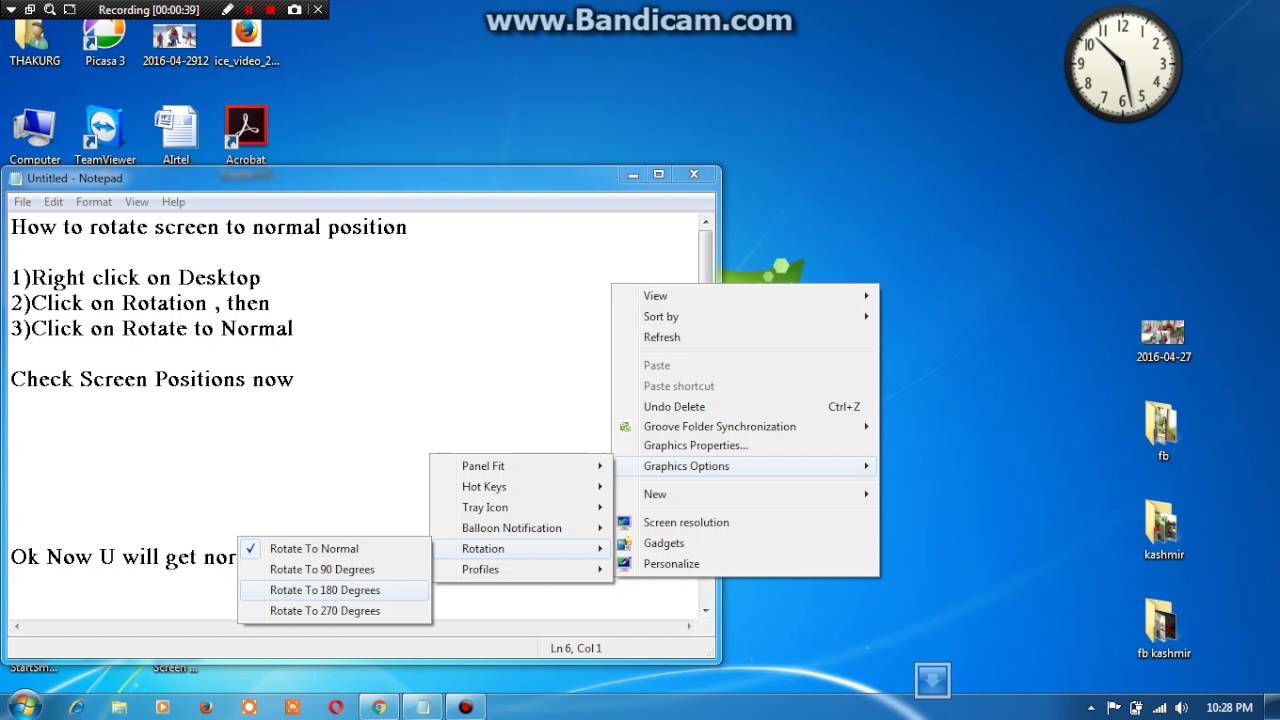
- #Screen position screenx screeny screenh screenw how to
- #Screen position screenx screeny screenh screenw install
#Screen position screenx screeny screenh screenw install
Pillow needs to be installed, and on Linux you may need to install additional libraries to make sure Pillow's PNG/JPEG works correctly. Linux needs the python3-xlib (or python-xlib for Python 2) module installed. OS X needs the pyobjc-core and pyobjc module installed (in that order).
The Win32 extensions do not need to be installed. If you are installing screen_search from PyPI using pip: Type in your Terminal pip install screen_search Screen_search is small python library use to Searchs for an image on the screen install: Now, what about the scale of the object!?. That's wasn't so hard was it! ) All you have to do now is test if the screen position is outside the screen boundary (taking the object's size into account!), then make it invisible and ignore it. Just remember that ScreenZ is from the player at 0,0,0, and so is ObjectZ. ) The point at which the ray intersects the screen can also be found like this: Now, all that said, you can shoot me later, because there is another way. | ScreenY = 25 (25 pixels up from screen center, or ScreenCenterY - ScreenY) | ScreenY = tan(verticalAngleToObject ) zDistanceToScreen Now let's do this for screen's vertical position: | ScreenX = -25 (25 pixels to the left of screen center, or ScreenCenterX + ScreenX) Good, now we know what HORIZONTAL angle the object is at. | horizontalAngleToObject = -26.565° (0° is straight ahead) | horizontalAngleToObject = atan(-100/200) These examples are all contrived and nothing realistic! ) ) Screen distance from player (z): 50 pixels (units can be whatever you want, just be consistent - since I'm doing a 1:1 position for objects within the screen space, my depth is using the same unit. Okay, so let's put this all together and find the screen position of the circle!Ĭircle object position: -100,100,200 (x,y,z - in pixels) ['z' would be a new instance variable added) | ScreenY = tan(verticalAngleToObject) zDistanceToScreen | ScreenX = tan(horizontalAngleToObject) zDistanceToScreen The screen x = distance from player (0,0), to the screen center (0,z), times tangent of the angle towards the object, so:
#Screen position screenx screeny screenh screenw how to
Can you figure out now how to find the screen pixel's 'x' for the circle knowing the above? ) You already have the formula. At a given distance of 'a' (or 'z') we can find 'x'! Now, that's all fine, but remember, we want the SCREEN position, which is where the 'h' line crosses the blue line (the screen). The 'a' here represents the depth ('z'), and the 'o' represents the 'x' position. This gives the circle's angle from the 0,0 (x,y) point, but we want the 'o' part, which is: | tan(angle) = o/a (FYI: I'll be working in degrees, and not radians) The basic formula for finding the angle of 'h', given 'a' and 'o' is the following: So, let's look at the 'a', 'o', and 'h' lines in the image above. We can see here then how the angle and the scale factor seem related! The trick is finding out what "W" is at a object's given distance, then working backwards* towards the screen! Let's get into a bit of trig. If 'W' was 0.5, then every Z position would give Z0.5 for X, or HALF of Z (and the angle would be half as well). | X = Z W, where 'W' here is the horizontal scale factor.įor example, if W=1, then at a distance of 100 away from the player, the X position is the same, which is a line at a 45° angle (the thicker black lines in the image above). On the X/Z plane, the object's X position is proportional to the object's Z position. It's much easier to look at one plane at a time, so let's explore the X/Z plane. The object drawn on this "window" would reflect, in 2D space, where the object is in 3D. The screen itself is at a DIFFERENT position in front of the player (again, like a window). First, we can assume that any object anywhere, should become 0 when translated to the starting point (where the player's eye is), so:īut, of course, ALL objects will be drawn at screen position 0,0 (center of the screen). First, let's say the player's eye is at position 0,0,0 (x,y,z), and the object (the circle in the image above) is at -100,100,200 (x,y,z).


 0 kommentar(er)
0 kommentar(er)
